もくじ
はじめに
今回は、メールマーケティングにおいて統計学の知識が具体的にどういった場面で、役に立つのかいくつか紹介しようと思います。
統計学を勉強する上で、実践のイメージを持っていると、知識の取得の意欲も高まると思いますし、今回紹介したもの以外でも「これ何かに使えるんじゃないかな?」と考えながら学習していくヒントになるのではないかと思うので、読み終わったあと参考にしていただければ幸いです。
シンプソンのパラドックス

まずは、以下の図を見てください。これば、よくあるメルマガ送信後の開封に関する集計結果のレポートの例になります。
| メール件名 | 配信対象人数 | 開封人数 | 開封率 |
|---|---|---|---|
| 貴方様限定!商品◯◯! | 10000 | 2000 | 20% |
| 300円クーポン! | 10000 | 1500 | 15% |
レポートの結果から、今回のメルマガに関しては、「クーポンよりも商品名を入れた訴求」の方が開封に対して効果があったと見ることができます。
では、次に今度は別のメルマガ送信後の開封に関する集計結果のレポートの例を見てみましょう。
| ライトユーザ | ヘビーユーザ | |||||
|---|---|---|---|---|---|---|
| メール件名 | 配信対象人数 | 開封人数 | 開封率 | 配信対象人数 | 開封人数 | 開封率 |
| A | 2000 | 200 | 10% | 8000 | 1800 | 22.5% |
| B | 9000 | 1200 | 13.33% | 1000 | 300 | 30% |
ライトユーザ・ヘビーユーザと言ったユーザ毎の商品の購入履歴に応じたセグメントを追加したので前のレポートと比較して少し複雑になってます。
メールの件名に関しては、ここでは一旦「A」「B」として伏せています。
前のグラフと同様に各件名ごとの開封率を見てみましょう。
ライトユーザに関しては、Bの方が開封率が高くなっています。ベビーユーザに関してもBの方が開封率が高くなっています。
よって、この場合だと、レポートの結果から、今回のメルマガに関しては「A」よりも「B」の方が開封に対して効果があったと見ることができます。
2つのグラフを再度並べてみます。
| メール件名 | 配信対象人数 | 開封人数 | 開封率 |
|---|---|---|---|
| 貴方様限定!商品◯◯! | 10000 | 2000 | 20% |
| 300円クーポン! | 10000 | 1500 | 15% |
| ライトユーザ | ヘビーユーザ | |||||
|---|---|---|---|---|---|---|
| メール件名 | 配信対象人数 | 開封人数 | 開封率 | 配信対象人数 | 開封人数 | 開封率 |
| A | 2000 | 200 | 10% | 8000 | 1800 | 22.5% |
| B | 9000 | 1200 | 13.33% | 1000 | 300 | 30% |
A,Bの配信対象人数と開封人数を合計してみると一致するので、既に気づいてるかもしれませんが、この2つのグラフは同じメルマガの配信結果のレポートになります!
違いはライトユーザ、ヘビーユーザのセグメントを追加しただけです。
| メール件名 | 配信対象人数 | 開封人数 | 開封率 |
|---|---|---|---|
| 貴方様限定!商品◯◯! | 10000 | 2000 | 20% |
| 300円クーポン! | 10000 | 1500 | 15% |
| ライトユーザ | ヘビーユーザ | |||||
|---|---|---|---|---|---|---|
| メール件名 | 配信対象人数 | 開封人数 | 開封率 | 配信対象人数 | 開封人数 | 開封率 |
| 貴方様限定!商品◯◯! | 2000 | 200 | 10% | 8000 | 1800 | 22.5% |
| 300円クーポン! | 9000 | 1200 | 13.33% | 1000 | 300 | 30% |
各レポートでの、開封率の評価に戻ります。
上のグラフでは、「クーポンよりも商品名を入れた訴求」の方が開封に対して効果があったと考察していました。
しかし、下のグラフでは、「商品名よりもクーポンを入れた訴求」の方が開封に対して効果があったと考察することができます。
同じメルマガの内容に関するレポートなのに考察が両者で逆になってることがわかります。
このように、「全体で見たときと分割してみたときの結果は必ずとも一致しない」数学的な現象は「シンプソンのパラドックス」として呼ばれています。
レポートで、メールマーケティングの各パラメータの結果の考察を出す場合、顧客の属性情報等のセグメントでの切り分けをしない全体での判断、評価だけをしてしまうと、切り分けをした場合の結果と異なる考察をしてしまう場合があります。
しかも、セグメントの切り分けをしないわけなので、その異なる考察には気づかないままになってしまいます。
ベルヌーイ分布と仮説検定

今度は、クリック率のレポートについて見ていきます。
あるメルマガでABテストを行い、2種類のコンテンツの出し分けを行いクリック結果のレポートを出したものです。
| メールコンテンツ | クリック率 |
|---|---|
| A | 2.00% |
| B | 1.80% |
| メールコンテンツ | クリック率 |
|---|---|
| A | 25.00% |
| B | 36.00% |
上のグラフだと、クリック率の差異は「0.2%」で、下のグラフだと、クリック率の差異は「11%」となっています。
この数値だけを見て考察すると、上のグラフだと、「コンテンツを変えても効果がなかった」下のグラフだと「コンテンツを変えると効果があった」と言った結論になるかと思います。
ただ今回は、もう少し統計的な考察を追加してみたいと思います。
※以下は大学以上の数学の知識を使用しているので、正確に説明しようとするとかなり長くなってしまうので(数学的な理論はあまりこの記事の本質ではないことから)、簡略化して説明しています。
まず、クリック人数という値についてですが、数学的にはクリックした人を「1」、クリックしなかった人を「0」の値でみなすことができます。
ここでメールが送られてきて、クリックをするという行為を、以下のように考えます。
メールが送られてきてきたユーザが一人ひとり、メールコンテンツが持ってるクリック率pに基づいて行動する。
具体的には確率 p で クリックし 、確率 1 − p で クリックしないアクションを取る。
これは、統計学の確率分布で言うベルヌーイ分布(確率 p で 1 、確率 1 − p で 0 をとる)とほぼ同じ動きとみなせる。
次にA/Bテストにおける仮説検定を行います。
仮説検定とはある仮説に対して、それが統計学的に正しいのか検証する手法のことを言います。
今回のケースでは以下のように考えます。
調べる内容:クリック率の違いが「メールのクリエイティブの違いによるものなのか」、それとも「たまたまそうなっただけで違いがあるとは言えない」のかを調べる
メールのクリエイティブの違いはないと仮定します。この場合、クリックする確率pはA,B同じであると仮定することになります。
ここから、結果のクリック率の差が、この仮定のもとでどれ位珍しいことなのかを数値として算出します。
この珍しさの値は高ければ高いほど、このクリック率の差が偶然発生することが珍しいと言えることになります。
この珍しさの値が一定値を超えたばあい、つまり偶然発生すると考えるにはあまりに珍しい確率であるとみなせる場合、最初にたてた仮定が間違っているとみなすことができます。
最初の仮説とは「メールのクリエイティブの違いはない」というものだったので、つまりこのクリック率の違いは、偶然発生したものではなく、メールコンテンツによる違いであると結論づけることができます。
以上が、まず考え方の流れになります。
次に説明に出てきた「珍しさの値」についてですが、具体的には以下の数式で算出します(導出方法については省略します)。
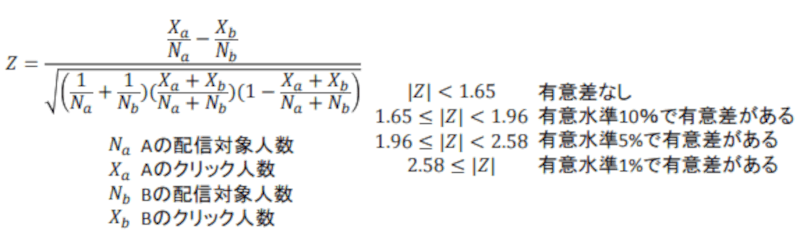
記号が多く分かりづらいと思いますが、分母はクリック人数を配信対象人数で割ったものの差異をだしているので、これはクリック率の差異になります。
一方で分母には、配信対象人数や全配信人数でのクリック率のパラメータも入っています。「珍しさの値」についてはこれらの分母のパラメータも影響を与えています。
このZ=「珍しさの値」ですが、統計学では「1.65」「1.96」「2.58」辺りの値を判断の境界値として採用することが多いです。
また「珍しさの値」は絶対値での評価をします。
統計的に、偶然発生したものではないとみなすことができた場合、「有意差がある」と表現します。
先程の3つの値は各それぞれの有意差の水準となるもので、使用した値に応じて「有意水準10%で有意差がある」「有意水準5%で有意差がある」「有意水準1%で有意差がある」と表現します。
それでは、今回説明した統計的な考察を2つのクリック率のABレポートでしてみましょう。
有意水準による考察をするため、先程のグラフでは表示していなかった配信対象人数とクリック人数を追加したグラフを元に計算します。
| メールコンテンツ | クリック率 | 配信対象人数 | クリック人数 |
|---|---|---|---|
| A | 2.00% | 350000 | 7000 |
| B | 1.80% | 350000 | 6300 |
この場合、Z=6.13となり「有意水準1%で有意差がある」といえます。
| メールコンテンツ | クリック率 | 配信対象人数 | クリック人数 |
|---|---|---|---|
| A | 25.00% | 40 | 10 |
| B | 36.00% | 200 | 72 |
この場合、Z=-1.34となり「有意差なし」といえます。
統計的にみると、クリック率の差が殆どなくても、配信対象人数の母数が大きいと有意な差を見つけることができて、逆にクリック率の差が大きくあったとしても配信対象人数の母数が小さいと有意な差は得られないことがわかると思います。
今回のように、クリック率の差による評価だけで考察をすると、配信母数が少なくて、統計的に有意な差ではなくとも、効果があったかのような判断をしてしまうことがあります。
逆に、統計的知見があると、クリック率の差が果たして効果があったと判断するに足るものなのかの判断を正確にすることができます。
カイ二乗検定による仮説検定

最後に、先程紹介した仮説検定の別パターンでの利用方法についても簡単に紹介しようと思います。
今回は題材がメルマガではなくWeb訪問履歴になるのですが、いろいろなマーケティング分野に応用が効く考え方ではないかと思うので、参考にしていただければと思います。
下図はあるユーザの曜日毎のWeb訪問数になります。
| 曜日 | 月 | 火 | 水 | 木 | 金 | 土 | 日 | 合計 |
|---|---|---|---|---|---|---|---|---|
| 回数 | 6 | 4 | 3 | 5 | 6 | 10 | 8 | 42 |
このユーザが曜日によって、Webサイトを訪れるのに差があるのか、例えば平日より土日のほうが訪れやすいといった傾向があるのかについて調べてみたいと思います。
※以下は前回と同様に、大学以上の数学の知識を使用しており、正確に説明しようとするとかなり長くなってしまうので、簡略化して説明することにします。
先程のクリック率と同様に仮説検定を行います。
仮説は、「曜日によって訪問数に差はない」とします。この場合の期待回数は42 ÷7 = 6回となります。
もし、仮に曜日によって訪問数に差はないとした場合、最も期待させる可能性としてはすべての曜日に同じ回数、すなわち6回訪問している状態になります。
実際の状態は、すべての曜日の値が6にはなってないわけですが、ではこの実際の値は最も期待できる状態からどれぐらい乖離した状態なのか、その乖離している量について調べます。
この「どれくらい乖離しているかの量」のことを統計的にはカイ二乗統計量といいます。
カイ二乗統計量は各値と期待値の差の二乗の合計で算出されます。
今回のケースでは、具体的には以下の数式で算出します。
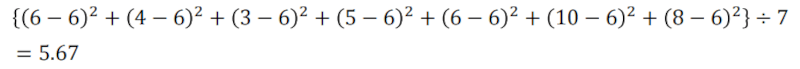
詳細はかなり長くなってしまうので割愛しますが、今回の統計量は自由度6のカイ2乗分布と呼ばれるものに従います。
この自由度6のカイ2乗分布の上側5%点は12.59となっておりこの数値とカイ二乗統計量を比較します。
5.67は12.59より小さいので、この仮説は偶然ではないとみなすことができません。
よって、このお客様は曜日によって訪問数に差があるとは言えなことになります。
(以上の流れのことをカイ二乗検定といいます)
さいごに
今回は、メルマガ等のレポーティングで使われる統計的な考察についていくつか簡単に説明しました。他にも有用そうなトピックがあれば、また紹介しようと思います。
トライコーンでは、グループ企業である株式会社セプテーニ(※)と共に、Salesforce Marketing Cloudの 導入支援・活用支援サービスを提供しております。 デジタル広告代理店として、ウェブマーケティングや運用型広告で20年以上の実績をもつセプテーニと、25年以上にわたるCRM・Webマーケティング支援活動で培ったトライコーンのノウハウを基に、顧客獲得から優良顧客への育成・維持まで、広範囲にわたりお客様のビジネスの成功を支援いたします。
※株式会社セプテーニは株式会社セールスフォース・ジャパンの Salesforce Marketing Cloud コンサルティングパートナーの認定企業です。 ※「Salesforce」「Salesforce Marketing Cloud」「Marketing Cloud Engagement」「Marketing Cloud Account Engagement」「Marketing Cloud Personalization」「Marketing Cloud Customer Data Platform」「Marketing Cloud Intelligence」は、Salesforce.com Inc.の登録商標です。


